Type I and Type II Errors
A null hypothesis is either true or false. Unfortunately, we do not know which is the case, and we rarely will. We therefore cannot talk about the probability of the null hypothesis being true or false because there is no element of chance: it is either true or false. You may not know whether the null hypothesis is true or false, but that is just a lack of knowledge; it is one or the other.
For example, if you are testing whether a potential mine has a greater gold concentration than that of a break-even mine, the null hypothesis is that the potential mine has a gold concentration no greater than a break-even mine. That hypothesis is either true or false; you just don’t know which. There is no probability associated with these two cases (in a frequentist sense) because the gold is already in the ground. As a result, there is no possibility of chance because everything is already set. All we have is our own uncertainty about the null hypothesis.
This lack of knowledge about the null hypothesis is why we need to perform a statistical test: we want to use our data to make an inference about the null hypothesis. Specifically, we need to decide if we will act as if the null hypothesis is true or if it is false. From our hypothesis test, we therefore choose to accept or reject the null hypothesis. If we accept the null hypothesis, we are stating that our data are consistent with the null hypothesis (recognizing that other hypotheses might also be consistent with the data). If we reject the null hypothesis, we are stating that our data are so unexpected that they are inconsistent with the null hypothesis.
Our decision will change our behavior. If we reject the null hypothesis, we will act as if the null hypothesis is false, even though we do not know if that is in fact false. If we accept the null hypothesis, we will act as if it is true, even though we have not demonstrated that it is true. This is a critical point: regardless of the results of our statistical test, we will never know if the null hypothesis is true or false. In other words, we do not prove or disprove null hypotheses, and we never will. We can never claim that null hypotheses are true or false.
In short, we operate in a world where hypotheses are true or false, but we don’t know which. We will perform statistical tests that allow us to make decisions (accept or reject the null hypothesis) based on the available data. We would like these to be correct decisions, so we need to make choices that minimize the possibility of error.
There are four possible scenarios because we have two possibilities for the null hypothesis (true or false) and two possibilities for our decision (accept or reject). Two of these are correct decisions: we could accept a true null hypothesis or reject a false null hypothesis. The other two cases are errors. We have committed a type I error if we reject a true null hypothesis. We have made a type II error if we accept a false null hypothesis.
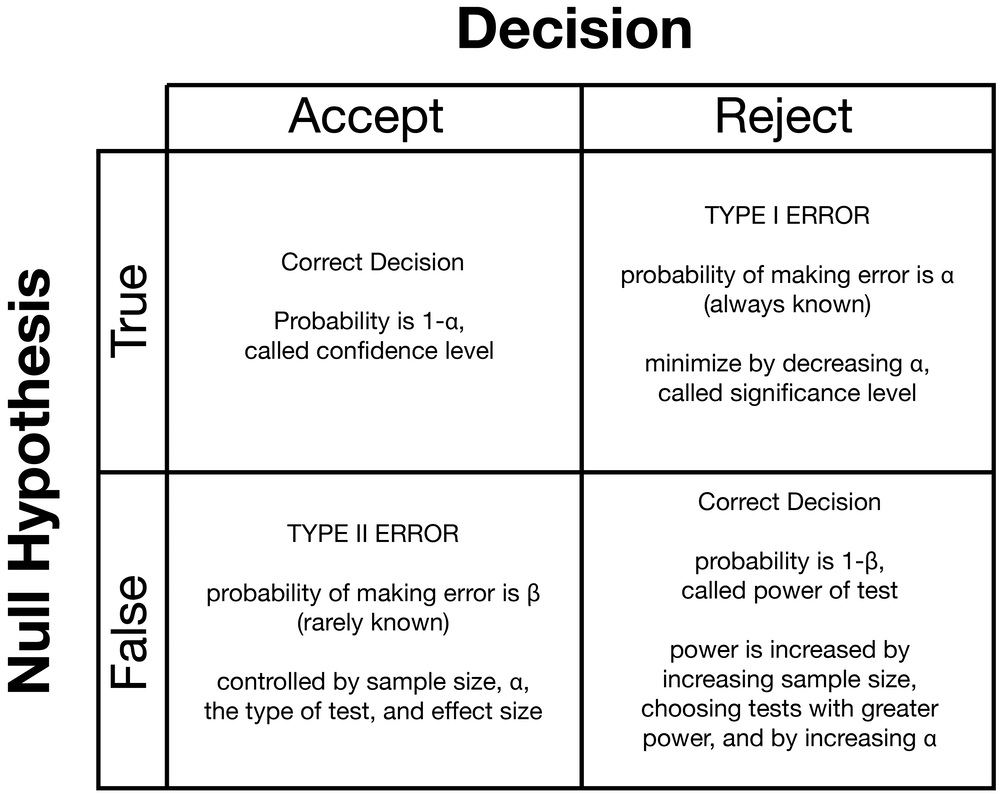
Each of these four possibilities has a probability of occurring, and those probabilities depend on whether the null hypothesis is true or false.
If the null hypothesis is true, there are only two possibilities: we may reject it with a probability of alpha (α), or we will choose to accept the null hypothesis with a probability of 1-α. Rejecting a true null hypothesis is called a false positive, such as when a medical test says you have a disease when you do not.
If the null hypothesis is false, there are likewise only two possibilities: we may accept the null hypothesis with a probability of beta (β), or we will reject it with a probability of 1-β. Accepting a false null hypothesis is called a false negative, such as when a medical test says you do not have a disease when you actually do.
Because the probabilities depend on whether the null hypothesis is true or false, the probabilities in each row sum to 100%. The probabilities in each column do not sum to 100%, except by extraordinary coincidence.
We need to lessen the chances of making both error types because we don’t know the truth of a null hypothesis. If the null hypothesis is true, we want to decrease our chance of making a type I error: we want to find ways to reduce alpha. In case the null hypothesis is false, we want to lessen our chance of making a type II error: we want to find ways to reduce beta. Because we will never know if the null hypothesis is true or false, we need a strategy for doing both, of simultaneously keeping the probabilities of alpha and beta as small as possible.
Significance and confidence
Keeping the probability of a type I error low is straightforward because we choose our significance level (α). If we are especially concerned about making a type I error, we can lower our significance level to be as small as we wish.
If the null hypothesis is true, we have a 1-α probability that we will make the correct decision and accept it. We call that probability (1-α) our confidence level. Confidence and significance sum to one because rejecting and accepting a null hypothesis are the only possible choices when the null hypothesis is true. Therefore, when we decrease significance, we increase our confidence. Although you might think you would always want confidence to be as high as possible, doing so comes at a high cost: we make type II errors more likely.
Beta and power
Keeping the probability of a type II error small is more complicated.
When the null hypothesis is false, β is the probability that we will make the wrong choice and accept it (a type II error). Beta is nearly always unknown since knowing it requires knowing whether the null hypothesis is true or not. Specifically, calculating beta requires knowing the true value of the parameter, that is, the true hypothesis underlying our data. Knowing that is an impossibility; moreover, if we knew the true value, we wouldn’t need statistics.
If the null hypothesis is false, there is a 1-β probability that we will make the right choice and reject it. Statistical power is the probability that we will make the right choice when the null hypothesis is false. Power reflects our ability to reject false null hypotheses and detect new phenomena in the world. We must try to maximize power. Four factors control power:
- Power increases with the size of the effect that we are trying to detect. For example, if we are trying to detect a large difference in means, that will be easier than trying to detect a small difference; in other words, we have greater power if the difference (the effect size) is large. We cannot control effect size because it is determined by the problem we are studying. The remaining three factors, however, are entirely under our control.
- Sample size (n) has a major effect on power: increasing sample size increases power. We should always strive to have as large of a sample size as money and time allow, as this is the best way to increase power.
- Some statistical tests have greater power than other tests. In general, parametric tests (ones that assume a particular distribution, often a normal distribution) have greater power than nonparametric tests (those that do not assume a particular distribution).
- Our significance level affects β. Increasing alpha (significance) will increase our power but also increase the risk of rejecting a true null hypothesis.
Our strategy for minimizing errors
We keep the probability of committing a type I error small by keeping significance (α) as small as possible.
We keep our probability of committing a type II error small by (1) increasing sample size as much as possible, given the constraints of time and money, (2) choosing tests with high power, and (3) not making significance (α) too small. As a data analyst, you should always think of ways to do all three.
Tradeoffs in α and β
We would like to minimize the probability of making type I and type II errors, but there is a tradeoff in α and β: decreasing one necessarily increases the other. We cannot simultaneously minimize both, and we must prioritize one or the other. Which one we prioritize will depend on the circumstances.
For example, if we are in charge of quality control at a factory, our null hypothesis would be that the current production run meets some minimum quality standard. We want to maximize our profits, so we do not want to be overly careful and discard too many production runs; thus we set α to be low because Type I errors cost us money. α is thus known as producer’s risk. If we are a consumer, we do not want defective goods, so if the null hypothesis is false (the goods are defective), we want the manufacturer to catch this and not ship defective products to consumers; in other words, we want β to be low. β is therefore known as consumer’s risk.
Another example comes from court proceedings, and we need to contrast the burden of proof in criminal and civil trials.
In a criminal trial, it is the individual pitted against the state. The founders of our government did not want the state to be too powerful and take away the rights of innocent people, so the standard in a criminal trial is “proof beyond a reasonable doubt”. In effect, this sets α to be very low, accepting the risk that some guilty people will walk free (a type II error).
In civil trials, individuals are pitted against one another, and there is no reason to favor one party over another. The standard of proof is therefore “a preponderance of the evidence”, that is, whoever presents the stronger case wins. This makes alpha much larger, creating a greater balance between type I and type II errors. Errors will not preferentially favor one party or the other.
Type I and II errors therefore carry opposing risks. For scientists, a type I error causes us to think we have made an important discovery by finding something unusual in nature, but we have not. Think of the infamous 1989 report of cold fusion or any other discovery that proves to be incorrect. A type II error means we have missed a potential discovery: we should have detected that something was different from the null hypothesis, but we missed it because the power of our statistical test was too low.
Demonstration Code
This first block will demonstrate the relationship between alpha and beta for a small sample (n=20). This and the next block will generate color versions of the figures used in class.
dev.new(height=6, width=6) par(mfrow=c(2, 1)) # simulate Ho distribution for mean of small sample (n=20) nullMean <- 4.5 nullStandardDeviation <- 1.0 smallSample <- 20 iterations <- 10000 smallSampleMeans <- replicate(iterations, mean(rnorm(smallSample, nullMean, nullStandardDeviation))) # plot the distribution of the mean breaks <- seq(3, 6, 0.05) range <- c(min(breaks), max(breaks)) hist(smallSampleMeans, breaks=breaks, col="gray", main="Hypothesized Mean n=20", xlab="sample mean", xlim=range) # show the critical value alpha <- 0.05 criticalValue <- quantile(smallSampleMeans, 1-alpha) abline(v=criticalValue, col="blue", lwd=3) text(criticalValue, 800, "critical value", pos=4, col="blue") criticalValue # show alpha and 1-alpha text(5.5, 0, expression(alpha), cex=2, pos=3, col="blue") text(3.5, 0, expression(1-alpha), cex=2, pos=3, col="blue") # add an observed mean observedMean <- 5.1 arrows(observedMean, 600, 5.1, 50, angle=20, length=0.15, lwd=3, col="red") text(observedMean, 620, "observed mean", pos=4, col="red") # simulate true distribution for mean of small sample (n=20) # remember, this is unknowable to us trueMean <- 5.0 trueSd <- 1.0 trueSampleMeans <- replicate(iterations, mean(rnorm(smallSample, trueMean, trueSd))) # plot the distribution hist(trueSampleMeans, breaks=breaks, col="gray", main="True Mean (Unknowable)", xlab="mean", xlim=range) # copy the observed mean and the critical values arrows(observedMean, 600, 5.1, 50, angle=20, length=0.15, lwd=3, col="red") abline(v=criticalValue, col="blue", lwd=3) # show beta and 1-beta text(5.5, 0, expression(1-beta), cex=2, pos=3, col="blue") text(3.5, 0, expression(beta), cex=2, pos=3, col="blue") # Note that magic numbers were used for coordinates of arrows # and text labels. If you modify the code, you will likely # need to change these numbers
This second block will do the same, but for a large sample (n=60).
dev.new(height=6, width=6) par(mfrow=c(2, 1)) # simulate Ho distribution for mean of large sample (n=60) nullMean <- 4.5 nullStandardDeviation <- 1.0 largeSample <- 60 iterations <- 10000 largeSampleMeans <- replicate(iterations, mean(rnorm(largeSample, nullMean, nullStandardDeviation))) # plot the distribution of the mean breaks <- seq(3, 6, 0.05) range <- c(min(breaks), max(breaks)) hist(largeSampleMeans, breaks=breaks, col="gray", main="Hypothesized Mean n=60", xlab="sample mean", xlim=range) # show the critical value alpha <- 0.05 criticalValue <- quantile(largeSampleMeans, 1-alpha) abline(v=criticalValue, col="blue", lwd=3) text(criticalValue, 1400, "critical value", pos=4, col="blue") criticalValue # show alpha and 1-alpha text(5.5, 0, expression(alpha), cex=2, pos=3, col="blue") text(3.5, 0, expression(1-alpha), cex=2, pos=3, col="blue") # add an observed mean observedMean <- 5.1 arrows(observedMean, 1000, 5.1, 50, angle=20, length=0.15, lwd=3, col="red") text(observedMean, 1020, "observed mean", pos=4, col="red") # simulate true distribution for mean of large sample (n=60) trueMean <- 5.0 trueSd <- 1.0 trueLargeSampleMeans <- replicate(iterations, mean(rnorm(largeSample, trueMean, trueSd))) # plot the distribution hist(trueLargeSampleMeans, breaks=breaks, col="gray", main="True Mean (Unknowable)", xlab="mean", xlim=range) # copy the observed mean and the critical values arrows(observedMean, 1000, 5.1, 50, angle=20, length=0.15, lwd=3, col="red") abline(v=criticalValue, col="blue", lwd=3) # show beta and 1-beta text(5.5, 0, expression(1-beta), cex=2, pos=3, col="blue") text(3.5, 0, expression(beta), cex=2, pos=3, col="blue")
This third block is like the first (n=20), but shows a smaller effect size (that is, the actual mean is closer to hypothesized mean). This was shown in class, but it was not included on the handout.
dev.new(height=6, width=6) par(mfrow=c(2, 1)) # simulate Ho distribution for mean of small sample (n=20) nullMean <- 4.5 nullStandardDeviation <- 1.0 smallSample <- 20 iterations <- 10000 smallSampleMeans <- replicate(iterations, mean(rnorm(smallSample, nullMean, nullStandardDeviation))) # plot the distribution of the mean breaks <- seq(3, 6, 0.05) range <- c(min(breaks), max(breaks)) hist(smallSampleMeans, breaks=breaks, col="gray", main="Hypothesized Mean n=20", xlab="sample mean", xlim=range) # show the critical value alpha <- 0.05 criticalValue <- quantile(smallSampleMeans, 1-alpha) abline(v=criticalValue, col="blue", lwd=3) text(criticalValue, 800, "critical value", pos=4, col="blue") criticalValue # show alpha and 1-alpha text(5.5, 0, expression(alpha), cex=2, pos=3, col="blue") text(3.5, 0, expression(1-alpha), cex=2, pos=3, col="blue") # add an observed mean observedMean <- 5.1 arrows(observedMean, 600, 5.1, 50, angle=20, length=0.15, lwd=3, col="red") text(observedMean, 620, "observed mean", pos=4, col="red") # simulate true distribution for mean of small sample (n=20) # remember, this is unknowable to us trueMean <- 4.6 trueSd <- 1.0 trueSampleMeans <- replicate(iterations, mean(rnorm(smallSample, trueMean, trueSd))) # plot the distribution hist(trueSampleMeans, breaks=breaks, col="gray", main="True Mean (Unknowable)", xlab="mean", xlim=range) # copy the observed mean and the critical values arrows(observedMean, 600, 5.1, 50, angle=20, length=0.15, lwd=3, col="red") abline(v=criticalValue, col="blue", lwd=3) # show beta and 1-beta text(5.5, 0, expression(1-beta), cex=2, pos=3, col="blue") text(3.5, 0, expression(beta), cex=2, pos=3, col="blue")
You can download a pdf of the handout.
