THE BASICS OF CLOSURES IN SWIFT

01/08/2016

Closures are one of the great features in Swift. Closures build on blocks, which Apple introduced to iOS 4 in 2010. Blocks are lines of code that form a logical unit. For example, a completion block is a set of instructions that are invoked when a process has finished. A closure contains a block, but uses it as an object. In Swift, closures are first-class objects, meaning that they can be used like any other object, including as an argument to a function.

There are many great tutorials on closures in Swift. Most of these focus on Apple’s frameworks, but I want to start at a more basic level, simply to convey the idea that closures are code that you can pass to other functions. To do this, I won’t use Apple’s frameworks; instead, I’ll create my own functions and the closures they’ll use.

Let’s start by making a closure. A closure has a signature, that is, a list of parameters that it will take and what it will return. A signature has this form:

(oneArgument: itsType, anotherArgument: itsType) -> returnType

It’s one or more arguments in parentheses, with their types, followed by the type of what the closure will return. The simplest closure has no arguments and returns nothing, with a signature like this:

() -> Void

A closure that takes two strings as arguments and returns an integer (maybe, for example, the difference in their lengths) would have a signature like this:

(stringOne: String, stringTwo: String) -> Int

There could be many more arguments, too, and the return type could be more complicated, like a dictionary or a tuple. If the signature of a closure reminds you of a function, that’s good, because functions are a type of closure.

A closure also includes a block, a group of statements that will be executed. To separate the block from the signature, the signature is followed by the word in, then the lines of code. Combining the simplest signature with a very simple block would give something like this:

() -> Void in
print(“Eat more bacon”)

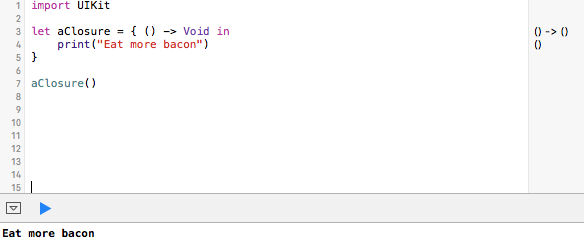
By convention, the “in” goes on the same line as the signature. As objects, closures can be named, and the entire closure (signature and block) is wrapped in curly quotes. The entire declaration of our closure (named aClosure) would look like this:

let aClosure = { () -> Void in
  print(“Eat more bacon”)
}

We can run this function, and it will execute, printing out “Eat more bacon” at the bottom left of the playground.

The value of closures isn’t just that they will execute, but that you can pass them to other functions, which can execute them:

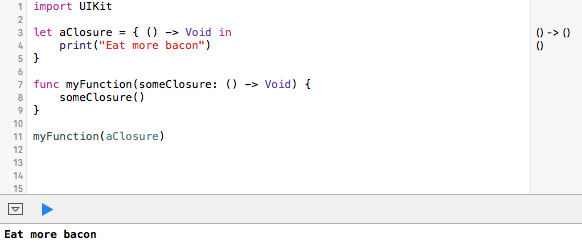
Here, I declared a new function called myFunction, which takes a named parameter (called someClosure) followed by the signature of a closure. In this case, it has the simplest signature, taking no arguments and returning nothing (Void). Any closure that matches this signature can be passed to this function. The function calls that closure by its parameter name (someClosure) and executes it; that is someClosure takes on the value of aClosure. Again, you can see at the bottom that “Eat more bacon” was printed to the console as expected.

That’s closures in a nutshell. They have a signature followed by a block of commands. They can have a name. They can be passed to other functions that accept a closure with a matching signature.

A more complicated example

It might not be obvious from this simple example why closures would be useful, but a slightly more complicated example can show you why.

Imagine that we wanted a function that would calculate the mean of an array of numbers. Imagine also that we might want to apply a transformation to those numbers before averaging them. For example, we might want to square those numbers if we were calculating a sum of squares. We might want to take the log of all those numbers to calculate the mean log. We might not want to change the values at all, that is, use the identify tranformation. It would be great to have a single function to calculate the mean, but as one of its arguments, be able to specify the transformation.

Of course, you might try to do all of this in one function, that is, have a switch statement or a bunch of if statements in your mean function that would do the appropriate transformation. As your list of possible transformations grows, though, your mean function will get more complicated. It would also become more difficult to test. It would be better to take a more modular approach, and closures let us do that.

Let’s think first about how to build our closures, each of which will handle one of the transformations. For the signature, we know that our closure should accept an array of Doubles (the original data), and that it should return an array of Doubles (the data after the transformation). Our signature should therefore look like this:

([Double]) -> [Double]

From that, it’s easy to build closures for an identity, square, and natural log transformation:

let identity = { (x: [Double]) -> [Double] in
  return x
}
 
let square = { (x: [Double]) -> [Double] in
  return x.map({ $0*$0 })
}
 
let naturalLog = { (x: [Double]) -> [Double] in
  return x.map({ log($0) })
}

Notice that each of these closures is named. The signature and in goes on the first line, and this is followed by the lines of code to be executed (the block). The signature and the block are wrapped in a set of curly quotes.

The identity closure is the easiest: it just returns what was input, unchanged. The code for the square and naturalLog closures may be more unfamiliar, but these could have been written just as easily using loops, where every value of the array was either squared or had its log taken. Instead, I used map, which itself uses a closure, albeit in a much more terse form. The map, filter, and reduce functions in Swift are amazing, and I highly recommend reading the posts on We Heart Swift and Electric Peel Software about them. These three functions let you bypass loops and write simple and efficient vectorized code.

Now that we have our closures, we can write our mean function, which will take these closures as an argument. The important part is that our function will have to have an argument which takes a closure with the [Double] -> [Double] signature.

func mean(x: [Double], transformation: [Double] -> [Double]) -> Double {
  let transformedX = transformation(x)
  let sum = transformedX.reduce(0.0, combine: +)
  let sampleSize = Double(transformedX.count)
  let theMean = sum / sampleSize
  return theMean
}

That’s a lot of Double’s in the first line, so let’s keep these straight. The first argument to our mean function is for the data (x), which will be an array of Doubles. The second argument will be for the tranformation closure, and it shows the signature that we need. Our mean function will return a Double, and that’s the final -> Double before the opening curly brace.

In the first line of our function, the data are transformed with transformation(x). Note that transformation is the name of the parameter in the function, and it will use whatever tranformation that is supplied to our function. The next line uses reduce to add (combine: +) all of these transformed values, starting with a value of zero. Calculating sample size and the mean is straightforward.

Running this in a playground shows our closures in action.

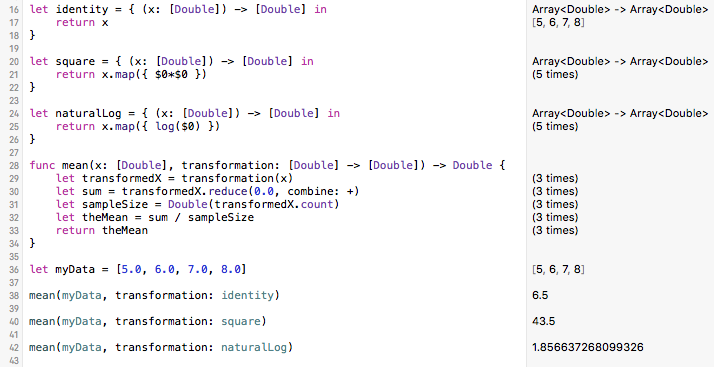
This is so much better than writing one function that has the logic for calculating each type of transformation as well as the logic for calculating the mean. First, using closures is more testable, because we can write separate tests for each closure and for the mean function. Second, closures make this problem much easier to build upon. If you need a new transformation, just write the closure, test it, and the mean function will work. If you need a new function, one that calculates the sum, or the standard deviation, or the variance, or the kurtosis, you needn’t repeat your tranformation code in each of those functions. Instead, just write each function to take a transformation closure with the matching signature.

Closures are an important part of Swift. Getting the most from Swift requires understanding them well.

Home