stratigrafia

DOUBLING TIME TO 10X TIME

3/26/20

Many of the recent articles on COVID-19 talk about the doubling time of the number of cases, but I wanted to think about it in terms of order of magnitude. The conversion is straightforward.

The starting point describes the number of cases at some time, N(t), by the number of cases at a starting time, N₀, and the time it takes for the number of cases to double, T_2x

 

 

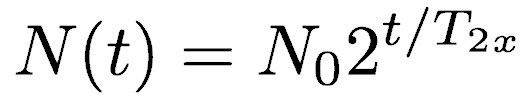
The same equation could be written for the number of cases at some future time when given the time for the number of cases to increase by a factor of 10, T_10x

 

 

Setting these two equal gives

 

 

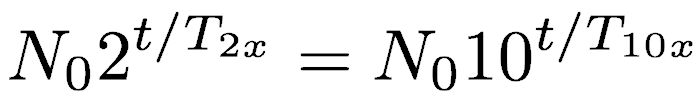
Cancelling the starting number of cases simplifies it to

 

 

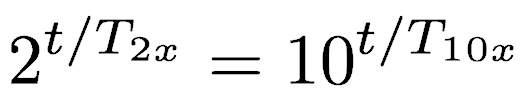
Taking the logarithm (any base) of both sides

 

 

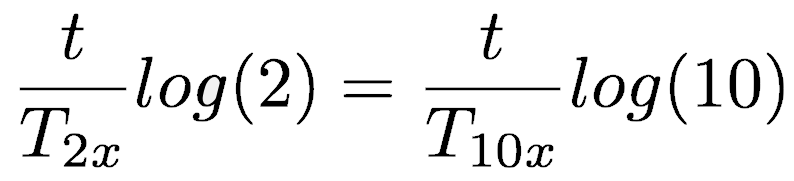
Removing t from both sides and solving for T_10x gives what we are after

 

 

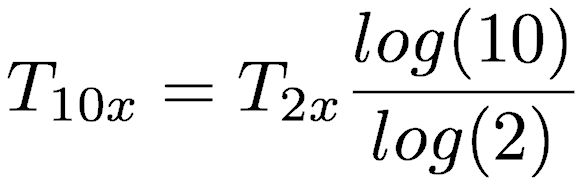
This could be generalized between any two scales, such as the tripling time and quadrupling time, if that’s your thing, man.

 

Home